What is Area?
The area is the region bounded by the shape of an object. The space covered by the figure or any two-dimensional geometric shape, in a plane, is the area of the shape. The area of all the shapes depends upon their dimensions and properties. Different shapes have different areas. The area of the square is different from the area of a kite.
If two objects have a similar shape then it’s not necessary that the area covered by them will be equal unless and until the dimensions of both shapes are also equal. Suppose, there are two rectangle boxes, with length as L1 and L2 and breadth as B1 and B2. So the areas of both the rectangular boxes, say A1 and A2 will be equal only if L1=L2 and B1=B2.
What is Perimeter?
Perimeter of a shape is defined as the total distance around the shape. Basically, perimeter is the length of any shape if it is expanded in a linear form. A perimeter is a total distance that encompasses a shape, in a 2d plane. The perimeter of different shapes can match in length with each other depending upon their dimensions.
For example, if a circle is made of a metal wire of length L, then the same wire we can use to construct a square, whose sides are equal in length.
What is the Difference Between Area and Perimeter?
Here is the list of differences between area and perimeter:
|
Area |
Perimeter |
| Area is the region occupied by a shape | Perimeter is total distance covered by the boundary of a shape |
| Area is measured in square units (m2, cm2, in2, etc.) | Perimeter is measured in units (m, cm, in, feet, etc.) |
| Example: Area of rectangular ground is equal to product of its length and breadth. | Example: Perimeter of a rectangular ground is equal to sum of all its four boundaries, i.e, 2(length + breadth). |
Area and Perimeter For all Shapes
There are many types of shapes. The most common ones are Square, Triangle, Rectangle, Circle etc. To know the area and perimeter of all these, we need different formulas.
Calculating Area and Perimeter for Different Shapes
Triangle
The formulas for calculating the perimeter and area of a triangle ABC are:
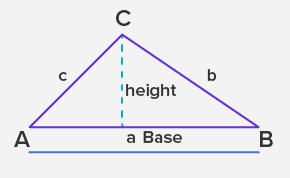
- Perimeter = a + b + c
⇒ Perimeter = sum of the length of all sides
⇒ Perimeter = a + b + c
- Area = 1⁄2 × base × height
Examples
1. Find the area and height of an equilateral triangle of side 12 cm. (√3 = 1.73).
Solution:
Area of the triangle = √3/4 a² square units
= √× 12 × 12
= 36√3 cm²
= 36 × 1.732 cm²
= 62.28 cm²
Height of the triangle = √3/2 a units
= √3/2 × 12 cm
= 1.73 × 6 cm
= 10.38 cm
2. Find the area of right angled triangle whose hypotenuse is 15 cm and one of the sides is 12 cm.
Solution:
AB² = AC² – BC²
= 15² – 12²
= 225 – 144
= 81
Therefore, AB = 9
Therefore, area of the triangle = ¹/₂ × base × height
= ¹/₂ × 12 × 9
= 54 cm²
3. The base and height of the triangle are in the ratio 3 : 2. If the area of the triangle is 243 cm² find the base and height of the triangle.
Solution:
Let the common ratio be x
Then height of triangle = 2x
And the base of triangle = 3x
Area of triangle = 243 cm²
Area of triangle = 1/2 × b × h 243 = 1/2 × 3x × 2x
⇒ 3x² = 243
⇒ x² = 243/3
⇒ x = √81
⇒ x = √(9 × 9)
⇒ x = √9
Therefore, height of triangle = 2 × 9
= 18 cm
Base of triangle = 3x
= 3 × 9
= 27 cm
Square
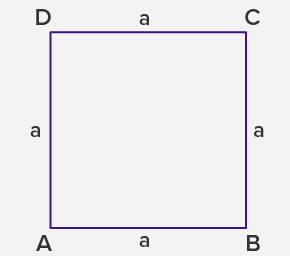
- Perimeter = 4a
⇒ Perimeter = sum of lengths of all sides
⇒ Perimeter = a + a + a + a
⇒ Perimeter = 4a
- Area = a2
⇒ Area = length × breadth
⇒ area = a × a
⇒ area = a2
where a is the length of the side of the square.
Examples
1. Find the perimeter and area of a square of side 11 cm.
Solution:
We know that the perimeter of square = 4 × side
Side= 11 cm
Therefore, perimeter = 4 × 11 cm = 44 cm
Now, area of the square = (side × side) sq. units
= 11 × 11 cm²
= 121 cm²
2. The perimeter of a square is 52 m. Find the area of the square.
Solution:
Perimeter of square = 52 m
But perimeter of square = 4 × side
Therefore, 4 × side = 52 m
Therefore, side= 52/4 m = 13m
Now, the area of the square = (side × side)
Therefore, area of the square = 13 × 13 m² = 169 m².
3. The area of a square is 144 m². Find its perimeter.
Solution:
Area of square = side × side
Given; area of square = 144 m²
Therefore, side² = 144 m²
Therefore, side = √(144 m²) = √(2 × 2 × 2 × 2 × 3 × 3) m² = 2 × 2 × 3 m = 12 m
Now, the perimeter of the square = 4 x side = 4 × 12 m = 48 m
4. The length of the diagonal of a square is 12 cm. Find its area and perimeter.
Solution:
Diagonal of a square = 12 cm
Area of square = 1/2 (d)²
= 1/2 (12)²
= 1/2 × 12 × 12
= 72
Side of a square = √Area
= √72
= √(2 × 2 × 2 × 3 × 3)
= 2 × 3√2
= 6 × 1.41
= 8.46 cm
Perimeter of square = 4 × 8.46 = 33.84 cm
5. The perimeter of a square courtyard is 144 m. Find the cost of cementing it at the rate of $5 per m².
Solution:
Perimeter of square courtyard = 144 m
Therefore, side of the square courtyard = 144/4 = 36 m
Therefore, area of square courtyard = 36 × 36 m² = 1296 m²
For 1 m², the cost of cementing = $5
For 1296 m², the cost of cementing = $1296 × 5 = $6480
Rectangle
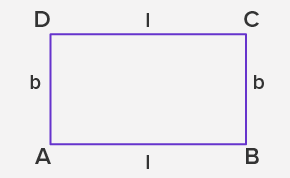
- Perimeter = 2 (l + b)
⇒ Perimeter = sum of lengths of all sides
⇒ Perimeter = l + b + l + b
⇒ Perimeter = 2 × (l + b)
- Area = l × b
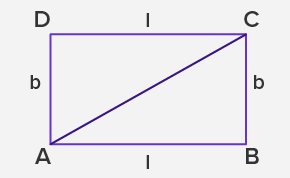
⇒ Area = Area (ABC) + Area (ADC)
⇒ Area = 2 × Area (ABC)
⇒ Area = 2 × (1⁄2 × base × height)
⇒ Area = base × height
⇒ Area = l × b
Examples
1. Find the perimeter and area of the rectangle of length 17 cm and breadth 13 cm.
Solution:
Given: length = 17 cm, breadth = 13 cm
Perimeter of rectangle = 2 (length + breadth)
= 2 (17 + 13) cm
= 2 × 30 cm
= 60 cm
We know that the area of rectangle = length × breadth
= (17 × 13) cm²
= 221 cm²
2. Find the breadth of the rectangular plot of land whose area is 660 m2 and whose length is 33 m. Find its perimeter.
Solution:
We know that the breadth of the rectangular plot = Area / Length
= 660 m² / 33 m
= 20 m
Therefore, the perimeter of the rectangular plot = 2 (length + breadth)
= 2(33 + 20) m
= 2 × 53 m
= 106 m
3. Find the area of the rectangle if its perimeter is 48 cm and its breadth is 6 cm.
Solution:
P = 2 (l + b)
Here, P = 48 cm; b = 6 cm
Therefore, 48 = 2 (l + 6)
⇒ 48 / 2 = l + 6
⇒ 24 = l + 6
⇒ 24 – 6 = l
⇒ 18 = l
Therefore, length = 18 cm
Now, area of rectangle = l × b = 18 × 6 cm² = 108 cm²
4. Find the breadth and perimeter of the rectangle if its area is 96 cm² and the length is 12 cm.
Solution:
Given, A = 96 cm² and l = 12 cm
A = l × b
Therefore, 96 = 12 × b
⇒ 96 / 12 = b
⇒ b = 8 cm
Now, P = 2 (l + b)
= 2 (12 + 8)
= 2 × 20
= 40 cm
5. The length and breadth of a rectangular courtyard is 75 m and 32 m. Find the cost of leveling it at the rate of $3 per m². Also, find the distance covered by a boy to take 4 rounds of the courtyard.
Solution:
Length of the courtyard = 75 m
Breadth of the courtyard = 32 m
Perimeter of the courtyard = 2 (75 + 32) m
= 2 × 107 m
= 214 m
Distance covered by the boy in taking 4 rounds = 4 × perimeter of courtyard
= 4 × 214
= 856 m
We know that area of the courtyard = length × breadth
= 75 × 32 m²
= 2400 m²
For 1 m², the cost of levelling = $3
For 2400 m², the cost of levelling = $3 × 2400
= $7200
6. A floor of the room 8 m long and 6 m wide is to be covered by square tiles. If each square tile is 0.8 m, find the number of tiles required to cover the floor. Also, find the cost of tiling at the rate of $7 per tile.
Solution:
Length of the room = 8 m
Breadth of the room = 6 m
Area of the room = 8 × 6 m²
{Area of room = Area of tiles that are put on the floor of the room.}
= 48 m²
Area of one square tile = 0.8 × 0.8 m² = 0.64 m²
Number of tiles required = Area of floor / Area of tiles
= 48 / 0.64
= (48 × 100) / 64
= 75 tiles
For 1 tile, the cost of tiling is $7
For 7 tiles, the cost of tiling is $(7 × 75) = $525
7. How many envelopes can be made out of a sheet of paper 100 cm by 75 cm, supposing 1 envelope requires 20 cm by 5 cm piece of paper?
Solution:
Area of the sheet = 100 × 75 cm² = 7500 cm²
Area of envelope = 20 × 5 cm = 100 cm²
Number of envelopes that can be made = Area of sheet / Area of envelope
= 7500 / 100
= 75 envelopes
8. A wire in the shape of rectangle of length 25 cm and breadth 17 cm is re-bent to form a square. What will be the measure of each side?
Solution:
Perimeter of rectangle = 2 (25 + 17) cm
= 2 × 42
= 84 cm
Perimeter of square of side x cm = 4x
Therefore, perimeter of rectangle = Perimeter of Square
84 cm = 4x
⇒ x = 21
Therefore, each side of square = 21 cm
These are the detailed step-by-step explanation with the formula of perimeter and area of rectangle.
9. The length and breadth of the rectangle park are in the ratio 5 : 4 and its area is 2420 m², find the cost of fencing the park at the rate of $10 per meter.
Solution:
Let the common ratio b x,
then length of rectangular park = 5x
Breadth of rectangular park = 4x
Area of rectangular park = 5x × 4x
= 20x²
According to the question,
20x² = 2420
⇒ x² = 2420 / 20
⇒ x² = 121
⇒ x = 11
Therefore, 5x = 5 × 11 = 55 and 4x = 4 × 11 = 44
So, the perimeter of the rectangular park = 2 (l + b)
= 2 (55 + 44)
= 2 × 99
= 198 cm
For 1 m, the cost of fencing = $10
For 198 m, the cost of fencing = $198 × 10
= $1980
Units of Measurement
If all the measurements are in centimeter, the units of measurement for the perimeter and area of different shapes are:
- Perimeter = sum of sides
Thus, the unit of measurement remains the same, as cm
- Area = product of sides
The unit of measurement is unit² or cm²
Area and Perimeter Formulas
Here is the list of the area and perimeter for different figures in a tabular form. Students can use this table to solve problems based on the formulas given here.
| Shape | Area | Perimeter | Terms |
| Circle | A = π × r2 | Circumference = 2πr | r = radius of the circle |
| Triangle | A = ½ × b × h | S = a+b+c |
b = base
h = height a,b and c are the sides of the triangle |
| Square | A = a2 | P = 4a | a = length of side |
| Rectangle | A = l × w | P = 2(l + w) |
l = length
w = width |
| Parallelogram | A = b × h | P = 2(a+b) |
a = side
b=base h=vertical height |
Applications of Area and Perimeter
We know that the area is basically the space covered by these shapes and perimeter is the distance around the shape. If you want to paint the walls of your new home, you need to know the area to calculate the quantity of paint required and cost for the same.
For example, to fence the garden in your house, the length required of the material for fencing is the perimeter of the garden. If it’s a square garden with each side as a cm then the perimeter would be 4a cm. The area is the space contained in the shape or the given figure. It is calculated in square units. Suppose you want to fix tiles in your new home, you need to know the area of the floor to know the no. of tiles required to cover the whole floor. In this article, let us have a look at the formula for area and perimeter of some basic shapes with diagrams and examples.
The concepts of area and perimeter are the basis for understanding Euclidean geometry and calculating the volume of solid shapes in 3-dimensional space such as cones, prism, sphere, and cylinder. Also, we use these formulas for calculating the area and perimeter for quadrilaterals and polygons comprising of sides and curves. The real-life utility of the concept is in several fields such as mapping, architecture, and surveying. The geometric representation of figures is done by sketching the distances and areas for clear understanding.
Three-dimensional objects derived from 2-dimensional shapes and land surveying in fields.
Fun Facts
- Different rectangles with the same perimeter can have different areas.
- Rectangles are also known as elongated squares.
- Perimeter for squares and rectangles is always less than their area, whereas it can be more than the area in case of triangles.