Area of the Path
The area of the path is the difference in the areas of the two rectangles. We will use the formula for the area of a rectangle to find the two areas. Then subtract the area of the smaller rectangle from the area of the bigger rectangle to find the required area of the path.
Formula Used: We will use the formula Area of rectangle = l × b, where l is the length of the rectangle and b is the breadth of the rectangle.
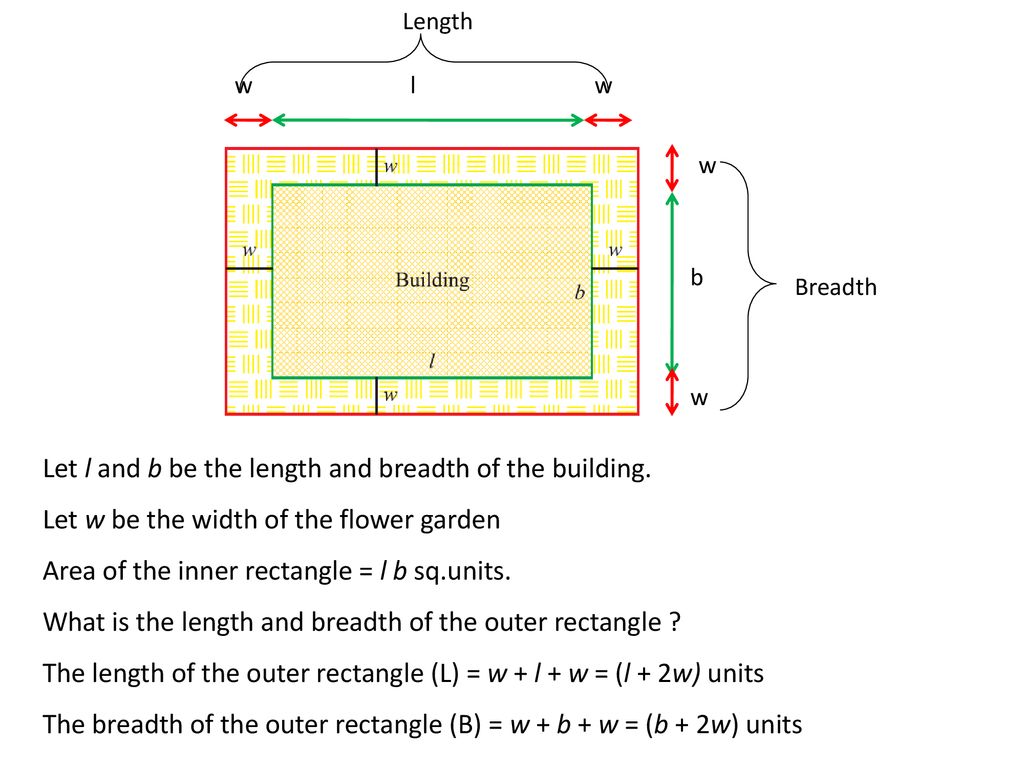
Examples on Area of the Path:
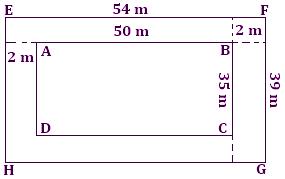
1. A rectangular lawn of length 50 m and breadth 35 m is to be surrounded externally by a path which is 2 m wide. Find the cost of turfing the path at the rate of $3 per m².
Solution:
Length of the lawn = 50 m
Breadth of the lawn = 35 m
Area of the lawn = (50 × 35) m²
= 1750 m²
Length of lawn including the path = [50 + (2 + 2)] m = 54 cm
Breadth of the lawn including the path = [35 + (2 + 2)] m = 39 m
Area of the lawn including the path = 54 × 39 m² = 2106 m²
Therefore, area of the path = (2106 – 1750) m² = 356 m²
For 1 m², the cost of turfing the path = $ 3
For 356 m², the cost of turfing the path = $3 × 356 = $1068
2. A painting is painted on a cardboard 19 cm and 14 cm wide, such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.
Solution:
Length of the cardboard = 19 cm
Breadth of the cardboard = 14 cm
Area of the cardboard = 19 × 14 cm² = 266 cm²
Length of the painting excluding the margin = [19 – (1.5 + 1.5)] cm = 16 cm
Breadth of the painting excluding the margin = 14 – (1.5 + 1.5) = 11 cm
Area of the painting excluding the margin = (16 × 11) cm² = 176 cm²
Therefore, area of the margin = (266 – 176) cm² = 90 cm²
3. A square flowerbed is surrounded by a path 10 cm wide around it. If the area of the path is 2000 cm², find the area of the square flower-bed.
Solution:
EFGH is the outer boundary of the path.
Let each side of the flowerbed = x cm
Then, the area of the square flowerbed ABCD (x × x) cm² = x² cm²
Now, the side of the square EFGH = (x + 10 + 10) cm = (x + 20) cm
So, the area of square EFGH = (x + 20) (x + 20) cm² = (x + 20)² cm²
Therefore, area of the path = Area of EFGH – Area of ABCD
= [(x + 20)² – x²] cm²
= [x² + 400 + 40x – x²] cm² = (40x + 400) cm²
But the area of path given = 2000 cm²
Therefore, 40x + 400 = 2000
⟹ 40x = 2000 – 400
⟹ 40x = 1600
⟹ x = 1600/40 = 40
Therefore, side of square flowerbed =40 cm
Therefore, the area of the square flowerbed = 40 × 40 cm² = 1600 cm²