In geometry, parallel lines can be defined as two lines in the same plane that are at equal distance from each other and never meet. They can be both horizontal and vertical.
We can see parallel lines examples in our daily life like a zebra crossing, the lines of notebooks, and on railway tracks around us.

Parallel lines
Two lines are said to be parallel if they do not intersect each other at any point in the plane. Lines are parallel if they are always the same distance apart (called “equidistant”), and will never meet. Just remember:
Always the same distance apart and never touching.
Parallel lines also point in the same direction.
What Do Parallel Lines Look Like?
In the figure below, line “AB” is parallel to the line “CD”.
The perpendicular distance is always the same between two parallel lines.

Sides of various shapes are parallel to each other. In the rectangle given below, the single arrow lines are parallel to each other, and similarly, the double arrow lines are also parallel to each other.
Parallel lines are represented with a pair of vertical lines between the names of the lines, using the sign: ︳︳
Parallel lines Examples from Real Life
If you observe your surroundings, you will encounter several parallel lines. Some common examples that you must watch next time are:
- The railway tracks run parallel to each other. They form two parallel lines or tracks for the wheels of the train to travel along on.
- The edges of a ruler are parallel to each other.
- Cricket stumps are parallel.
- Lines on a ruled paper are parallel.
- Zebra crossing has parallel white lines.
- The opposite boundaries of an eraser are parallel.
- Straight ceilings are parallel to floors.
- The queues in a bank are parallel to one other.
- The opposite sides of a rectangular or square-shaped object are parallel to each other.
Parallel Lines Cut by a Transversal
In geometry, a transversal is a line that intersects two or more lines. When a transversal cuts two parallel lines, several angles are formed. The angles are related as follows:

Exterior angles
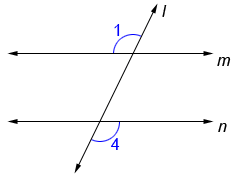
The angles that are situated outside of the line. Here, ∠1, ∠2, ∠7, and ∠8 are exterior angles.
Interior angles
The angles located inside of the lines are. Here ∠3, ∠4, ∠6, and ∠5 are interior angles.
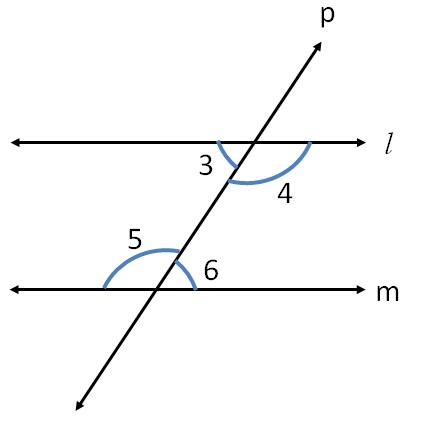
Corresponding angles
The angles that occupy the same relative position at each intersection. Here,
- ∠1 and ∠5
- ∠2 and ∠6
- ∠4 and ∠8
- ∠3 and ∠7 are corresponding pairs of angles.
We can often spot interior corresponding angles by drawing an F shape:
How to calculate with corresponding angles
In order to calculate with corresponding angles:
- Highlight the angle(s) that you already know.
- Use corresponding angles to find a missing angle.
- Use a basic angle fact to calculate the missing angle.
Alternate Interior angles
These angles are formed on the inside of two parallel lines when a transversal intersects them. The pairs of alternate interior angles are
- ∠3 and ∠5
- ∠4 and ∠6
We can often spot interior alternate angles by drawing a Z shape:
Alternate Exterior angles
These angles are formed on either side of the transversal outside the two parallel. The pairs of alternate exterior angles are
- ∠1 and ∠7
- ∠2 and ∠8

How to calculate with alternate angles
In order to calculate with alternate angles:
- Highlight the angle(s) that you already know.
- Use alternate angles to find a missing angle.
- Use a basic angle fact to calculate the missing angle.
Co-interior angles
These are also called interior angles on the same side or consecutive interior angles, or allied angles. Here, the co-interior angles are
- ∠4 and ∠5
- ∠3 and ∠6
Co-interior angles add up to 180º
We can often spot co-interior angles by drawing a C shape.
The two interior angles are only equal when they are both 90º.
In all other cases we can work out one of the co-interior angles by subtracting the other from 180º.
How to calculate with co-interior angles
In order to find a missing angle in parallel lines:
- Highlight the angle(s) that you already know.
- Use co-interior angles to find a missing angle.
- Use basic angle facts to calculate the missing angle.
Steps 2 and 3 may be done in either order and may need to be repeated. Step 3 may not always be required.
Vertically opposite angles
The pairs of vertically opposite angles are
- ∠1, and ∠3
- ∠2 and ∠4
- ∠5 and ∠7
- ∠6 and ∠8
Properties of Parallel Lines
The basic properties of parallel lines are as follows:
- They do not intersect with each other.
- Parallel lines do not meet, or they meet at infinity.
- They are always equidistant from each other.
How to Test If Two Lines are Parallel?
As shown above, when a transversal cuts two parallel lines at two distinct points, four angles are formed at a single point of intersection. In total, there are eight angles around two points of intersection.
The properties of parallel lines concerning transversals can be used for testing parallel lines. So, the two given lines will be parallel to each other if
- The corresponding angles are always equal to each other.
- Vertically opposite angles are equal.
- Alternate interior angles are equal.
- Alternate exterior angles are equal.
- Pair of co-interior angles on the same side of the transversal are supplementary, i.e., their sum is equal to 180 degrees.
Fascinating Facts
A triangle has no parallel lines, while a hexagon has three pairs of parallel lines. Think about other shapes and write down their number of parallel lines.