Cube of a number

If a number is multiplied by itself, we say that the number is squared. In the similar manner, if a number is multiplied by itself three times, we say that the number is cubed.

In other words, the square of a number when multiplied by the number itself gives the cube of the number. If n is the number, then cube of n is n × n × n (3 factors) and it is denoted by n^3. Thus, the exponent of the cube of a number is 3.

Perfect cube

In the above table, 1, 8, 27, …, 729 are called perfect cubes or perfect third powers of 1, 2, 3 , …, 9 respectively.

A natural number is said to be a perfect cube if it is the cube of some natural number.
If small numbers are given, we can identify whether it is a perfect cube or not. But if a larger number is given then it is difficult to do so. Hence, we need a method to check whether the number is a perfect cube or not.

Test for a Perfect Cube

Let us now have a look at the method:

We know that if a prime p divides a perfect cube, then p^3 also divides this perfect cube.

Also in the prime factorization of a perfect cube, every prime occurs 3 times or a multiples of 3 times. Thus, to check whether a number is a perfect cube or not,

i) We first prime-factorize the given number.
ii) Then group together triplets of the same prime factors.
iii) If no factor is left out, the number is a perfect cube. Otherwise, it is not a perfect cube.

Cube Root Formula

As we already know, the cube root gives a value which can be cubed to get the original value. Suppose, cube root of ‘a’ gives a value ‘b’, such that;

³√a = b This formula is only possible if and only if; a = b³

This formula is useful when we find the cubic root of perfect cubes.

Taking the cube root of the above cubes is very easy. But for imperfect cubes, we cannot evaluate the cube root this easily.

Hence, below is the table for different values of cube root, which students can memorize to solve the questions based on this concept.

How to Find Cube Root?

To find the cubic root of a number easily, we can use the prime factorization method. By evaluating the prime factors we can pair similar digits in a group of three and take them out as a single digit from the cubic root.

Let us take an example of finding the cube root of 8.

By factoring 8, we get; 8 = 2 x 2 x 2  = 2³

Now, if we take the cubic root both the sides, then the cube of 2 cancels the cubic root.

Hence, we get the value of ³√8

Therefore, ³√8 = 2

Examples:

1. Find the cube root of 64.

Solution:

To find the cube root of 64,

we need to use the prime factorization method.

64 = 2×2×2×2×2×2 64 = 4 × 4 × 4 64 = 4³

Now taking the cube root on both the sides, we get;

³√64 = ³√(4³)

³√64 = 4

2. What is the cube root of 1331?

Solution:

Using the prime factorization method,

we get;

1331 = 11×11×11 1331 = 11³

³√1331 = 11

3. Find the cube root of 216.

Solution:

By prime factorization,

we know;

216 = 2×2×2×3×3×3 216 = 2³×3³

216 = (2×3)³ = 6³

³√216 = 6

Cube root through prime factorization method

Step-1: Express the given number as the product of primes.

Step-2: Make groups in triplets of the same prime.

Step-3: Find the product of the primes choosing one from each triplet.

Step-4: The product from Step 3 is the required cube root of the given number.

Example: Find the cube roots of 512 and 531441.

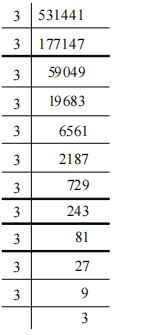
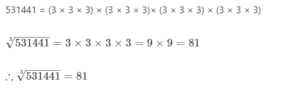
Example:

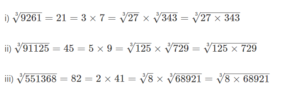
Cube roots of Positive Numbers

Let us now have a look at the method of finding cube roots of positive numbers.

The cube root of the product of two perfect cubes is the product of their cube roots.

Note: For two perfect cubes x and y,

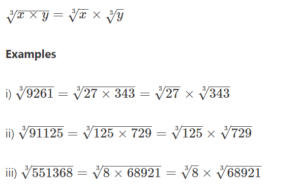
Cube roots of Negative Numbers

Let us observe the following examples

Cube root of a negative perfect cube is negative.