Trigonometry (from Greek trigonon “triangle” + metron “measure”).
Trigonometry is all about triangles.
Right-Angled Triangle
The triangle of most interest is the right-angled triangle. The right angle is shown by the little box in the corner:
Another angle is often labeled θ, and the three sides are then called:
- Adjacent: adjacent (next to) the angle θ
- Opposite: opposite the angle θ
- and the longest side is the Hypotenuse
Why a Right-Angled Triangle?
Why is this triangle so important?
Imagine we can measure along and up but want to know the direct distance and angle:
Trigonometry can find that missing angle and distance.
Or maybe we have a distance and angle and need to “plot the dot” along and up:
Questions like these are common in engineering, computer animation, and more.
And trigonometry gives the answers!
What is Trigonometry?
Trigonometry is the branch of mathematics concerned with specific functions of angles and their application to calculations. There are six functions of an angle commonly used in trigonometry. Their names and abbreviations are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc).
Trigonometry helps us in obtaining unknown angles and distances from known or measured angles in geometric figures, and is used a lot in science, engineering, video games, and more!
A right triangle has three sides, which can be uniquely identified as the hypotenuse, adjacent to a given angle (theta), or the opposite (theta) . A helpful mnemonic for remembering the definitions of the trigonometric functions is then given by “oh, ah, o-a,” “Soh, Cah, Toa,” or “SOHCAHTOA”, i.e.,
Sine equals opposite over hypotenuse,
(opposite side also known as Perpendicular)
Cosine equals adjacent over hypotenuse, and
Tangent equals opposite over adjacent,

Another mnemonic probably more common in Pakistan is “Some People Have, Curly Brown Hair, Tie Pant Black.”
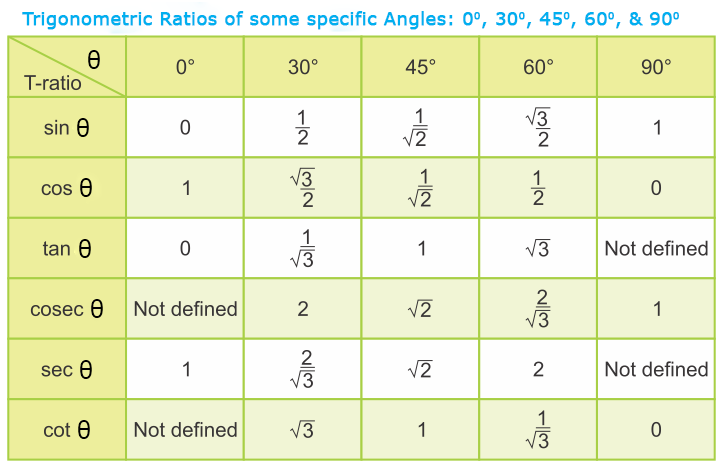
Example: What is the sine of 35°?
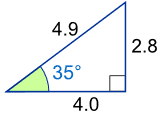
Using this triangle (lengths are only to one decimal place):
sin(35°) = Opposite / Hypotenuse = 2.8/4.9 = 0.57…
The triangle could be larger, smaller, or turned around, but that angle will always have that ratio.
Example: How Tall is The Tree?
The tree is 14.14 m tall.
Degrees and Radians
Angles can be in Degrees or Radians. Here are some examples:
| Angle | Degrees | Radians |
|---|---|---|
| 90° | π/2 | |
| __ Straight Angle | 180° | π |
| 360° | 2π |
Solving Triangles
Trigonometry is also useful for general triangles, not just right-angled ones . It helps us in solving triangles. “Solving” means finding missing sides and angles.
Example: Find the Missing Angle “C”
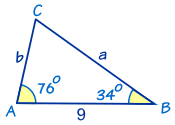
Angle C can be found using angles of a triangle added to 180°:
So C = 180° − 76° − 34° = 70°
We can also find missing side lengths. The general rule is:
When we know any 3 of the sides or angles we can find the other 3 (except for the three angles case).
Other Functions (Cotangent, Secant, Cosecant)
Similar to Sine, Cosine, and Tangent, three other trigonometric functions are made by dividing one side by another:

csc(θ) = Hypotenuse / Opposite
Secant Function:
sec(θ) = Hypotenuse / Adjacent
Cotangent Function:
cot(θ) = Adjacent / Opposite