What is a Subset ?

Set B is said to be a subset of Set A if all the elements of Set B are also present in Set A. In other words, set B is contained inside Set A.

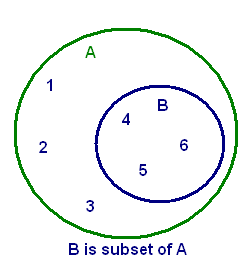
Example: If set A has {X, Y} and set B has {X, Y, Z}, then A is the subset of B because elements of A are also present in set B.

Subset Symbol

In set theory, a subset is denoted by the symbol ⊆ and read as ‘is a subset of’.

Using this symbol we can express subsets as follows:

A ⊆ B; which means Set A is a subset of Set B.

Note: A subset can be equal to the set. That is, a subset can contain all the elements that are present in the set.

All Subsets of a Set

The subsets of any set consists of all possible sets including its elements and the null set. Let us understand with the help of an example.

Example: Find all the subsets of set A = {1,2,3,4}

Solution: Given, A = {1,2,3,4}

Subsets =

{}

{1}, {2}, {3}, {4},

{1,2}, {1,3}, {1,4}, {2,3},{2,4}, {3,4},

{1,2,3}, {2,3,4}, {1,3,4}, {1,2,4}

{1,2,3,4}

Types of Subsets

Subsets are classified as

• Proper Subset
• Improper Subsets

A proper subset is one that contains a few elements of the original set whereas an improper subset, contains every element of the original set along with the null set.

For example, if set A = {2, 4, 6}, then,

Number of subsets: {2}, {4}, {6}, {2,4}, {4,6}, {2,6}, {2,4,6} and Φ or {}.

Proper Subsets: {}, {2}, {4}, {6}, {2,4}, {4,6}, {2,6}

Improper Subset: {2,4,6}

There is no particular formula to find the subsets, instead, we have to list them all, to differentiate between proper and improper one. 

What are Proper Subsets?

Set A is considered to be a proper subset of Set B if Set B contains at least one element that is not present in Set A.

Example: If set A has elements as {12, 24} and set B has elements as {12, 24, 36}, then set A is the proper subset of B because 36 is not present in the set A.

Proper Subset Symbol

A proper subset is denoted by ⊂ and is read as ‘is a proper subset of’. Using this symbol, we can express a proper subset for set A and set B as;

A ⊂ B

Proper Subset Formula

If we have to pick n number of elements from a set containing N number of elements, it can be done in ^NC_n number of ways.

Therefore, the number of possible subsets containing n number of elements from a set containing N number of elements is equal to ^NC_n.

How many subsets and proper subsets does a set have?

If a set has “n” elements, then the number of subset of the given set is 2ⁿ and the number of proper subsets of the given subset is given by 2ⁿ-1. 

Consider an example, If set A has the elements, A = {a, b}, then the proper subset of the given subset are { }, {a}, and {b}.

Here, the number of elements in the set is 2. 

We know that the formula to calculate the number of proper subsets is 2ⁿ – 1. 

= 2² – 1

= 4 – 1

= 3

Thus, the number of proper subset for the given set is 3 {{ }, {a}, {b}}.

Example: Find the number of subsets and the number of proper subsets for the given set A = {5, 6, 7, 8}.

Solution:

Given: A = {5, 6, 7, 8}

The number of elements in the set is 4

We know that,

The formula to calculate the number of subsets of a given set is 2ⁿ

= 2⁴ = 16

Number of subsets is 16

The formula to calculate the number of proper subsets of a given set is 2ⁿ – 1

= 2⁴ – 1

= 16 – 1 = 15

The number of proper subsets is 15.

What is Improper Subset?

A subset which contains all the elements of the original set is called an improper subset. It is denoted by ⊆.

For example: Set P ={2,4,6} Then, the subsets of P are;

{}, {2}, {4}, {6}, {2,4}, {4,6}, {2,6} and {2,4,6}.

Where, {}, {2}, {4}, {6}, {2,4}, {4,6}, {2,6} are the proper subsets and {2,4,6} is the improper subsets. Therefore, we can write {2,4,6} ⊆ P.

Note: The empty set is an improper subset of itself (since it is equal to itself) but it is a proper subset of any other set.

Superset 

In set theory, set A is considered as the superset of B, if all the elements of set B are the elements of set A. For example, if set A = {1, 2, 3, 4} and set B = {1, 3, 4}, we can say that set A is the superset of B. As the elements of B [(i.e.,)1, 3, 4] are in set A. We can also say that B is not a superset of A.

Superset Symbol

The superset relationship is represented using the symbol “⊃”. For instance, the set A is the superset of set B, and it is symbolically represented by A ⊃ B.

Consider another example,

X = {set of polygons}

Y = {set of irregular polygons}

Then X is the superset of Y (X⊃Y). In other words, we can say that Y is a subset of X (Y⊂X).

Properties of Superset

The important properties of superset are:

• Every set is considered as a superset of an empty set, as the null set has no elements in it. If A is the set, then it is represented as A ⊃ φ
• If A is the subset of B (A ⊂ B), then B should be the superset of set A (B⊃A).

Difference Between Superset and Subset

The major difference between superset and subset is that the superset and subset are opposite to each other. Let us assume, M and N are the two sets. If M is the superset of N, then we can say that N is the subset of M.

(i.e) M = {4, 7, 9} and N = {4, 9}

Thus, {4, 7, 9} is the superset of {4, 9}.

In other words, {4, 9} is the subset of {4, 7, 9}

The symbol to represent the superset is “⊃”, and the symbol that denotes the subset is “⊂”.

Example:

Let A = {a, e, i, o, u} and B = {a, c, d, e}. Is A a superset of B? And also, give reason.

Solution:

Given:

A = {a, e, i, o, u}

B = {a, c, d, e}

The set A is not a superset of set B because the elements “c and d” in set B are not present in set A. Hence, A is not a superset of B. We can also say that B is not a subset of set A.

Example:

If A = {2, 3, 7, 9} and B= {2, 7, 9}, then A is the proper superset of B. Justify.

Solution:

Given:

Set A = {2, 3, 7, 9}

Set B = {2, 7, 9}

Here A is the proper superset of set B, as all the elements of set B are in set A, but set A has one more extra element (i.e., 3) than set B.

Also, set A is not equal to set B.

Hence, A is the proper superset of set B.

Power Set

The power set is said to be the collection of all the subsets. It is represented by P(A).

If A is set having elements {a, b}. Then the power set of A will be;

P(A) =  {∅, {a}, {b}, {a, b}}

To learn more in brief, click on the article link of power set.

Properties of Subsets

Some of the important properties of subsets are:

• Every set is considered as a subset of the given set itself. It means that X ⊂ X or Y ⊂ Y, etc.
• We can say, an empty set is considered as a subset of every set. 
• X is a subset of Y. It means that X is contained in Y
• If a set X is a subset of set Y, we can say that Y is a superset of X