Square Root

The square root of a number is the inverse operation of squaring a number. The square of a number is the value that is obtained when we multiply the number by itself, while the square root of a number is obtained by finding a number that when squared gives the original number.

If ‘a’ is the square root of ‘b’, it means that a × a = b. The square of any number is always a positive number, so every number has two square roots, one of a positive value, and one of a negative value. For example, both 2 and -2 are square roots of 4.

However, in most places, only the positive value is written as the square root of a number.

Square Root Symbol

The square root symbol is usually denoted as ‘√’. It is called a radical symbol. To represent a number ‘x’ as a square root using this symbol can be written as:‘ √x ‘

where x is the number. The number under the radical symbol is called the radicand.

For example, the square root of 6 is also represented as radical of 6. Both represent the same value.

Square Root Formula

The formula to find the square root is:

Since, y.y = y² = a; where ‘a’ is the square of a number ‘y’.

Properties of Square root

Some of the important properties of the square root are as follows:

• If a number is a perfect square number, then there exists a perfect square root.
• If a number ends with an even number of zeros (0’s), then it can have a square root.
• The two square root values can be multiplied. For example, √3 can be multiplied by √2, then the result should be √6.
• When two same square roots are multiplied, then the result should be a radical number. It means that the result is a non-square root number. For instance, when √7 is multiplied by √7, the result obtained is 7.
• The square root of any negative numbers is not defined. Because the perfect square cannot be negative.
• If a number ends with 2, 3, 7 or 8 (in the unit digit), then the perfect square root does not exist.
• If a number ends with 1, 4, 5, 6 or 9 in the unit digit, then the number will have a square root.

It is very easy to find the square root of a number that is a perfect square. Perfect squares are those positive numbers that can be expressed as the product of a number by itself. in other words, perfect squares are numbers which are expressed as the value of power 2 of any integer.

We can use four methods to find the square root of numbers and those methods are as follows:

• Repeated Subtraction Method of Square Root
• Square Root by Prime Factorization Method
• Square Root by Estimation Method
• Square Root by Long Division Method

It should be noted that the first three methods can be conveniently used for perfect squares, while the fourth method, i.e., the long division method can be used for any number whether it is a perfect square or not.

Square Root by Repeated Subtraction Method

As per the repeated subtraction method, if a number is a perfect square, then we can determine its square root by:

• Repeatedly subtracting consecutive odd numbers from it
• Subtract till the difference is zero
• Number of times we subtract is the required square root

For example, let us find the square root of 25.

• 25 – 1 = 24
• 24 – 3 = 21
• 21 – 5 = 16
• 16 – 7 = 9
• 9 – 9 = 0

Since, the subtraction is done for 5 times, hence the square root of 25 is 5.

Square Root by Prime Factorization Method

Prime factorization of any number means to represent that number as a product of prime numbers.

To find the square root of a given number through the prime factorization method, we follow the steps given below:

• Step 1: Divide the given number into its prime factors.
• Step 2: Form pairs of similar factors such that both factors in each pair are equal.
• Step 3: Take one factor from the pair.
• Step 4: Find the product of the factors obtained by taking one factor from each pair.
• Step 5: That product is the square root of the given number.

Let us find the square root of 1764 by this method.

This method works when the given number is a perfect square number.

Square root by Estimation Method

This method is used as an approximation method, to find the square root by guessing the values.

For example, the square root of 4 is 2 and the square root of 9 is 3, thus we can guess, square root of 5 will lie between 2 and 3.

But, we need to check the value of √5 is nearer to 2 or 3. Let us find the square of 2.2 and 2.8.

• 2.2² = 4.84
• 2.8² = 7.84

Since the square of 2.2 gives an approximate value of 5, thus we can estimate the square root of 5 is equal to 2.2 approximately.

Square Root by Long Division Method

Finding square roots for the imperfect numbers is a bit difficult but we can calculate using a long division method. This can be understood with the help of the example given below. Consider an example of finding the square root of 962361.

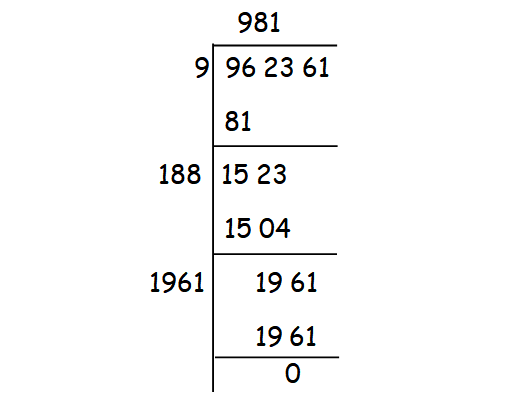
Thus, the square root of 962361 is 981.

There is very strong relation between squares and square roots as each one of them is the inverse relation of the other. i.e., if x² = y then x = √y. It can be simply remembered like this:

• When “square” is removed from one side of the equation, we get the square root on the other side. For example, 4² = 16 means, 4 = √16. This is also known as “taking square root on both sides”.
• When “square root” is removed from one side of the equation, we get square on the other side. For example, √25 = 5 means, 25 = 5². This is also known as “squaring on both sides”.