Circles

A circle is a curved plane figure. Every point on the circle is equidistant from a fixed point known as the center of the circle. It is a 2D shape and is measured in terms of radius. The word ‘Circle’ is derived from the Latin word ‘circulus’ meaning small ring.

A circle is a two-dimensional figure formed by a set of points that are at a constant or at a fixed distance (radius) from a fixed point (center) on the plane. The fixed point is called the origin or center of the circle and the fixed distance of the points from the origin is called the radius.

Circle Shaped Objects

There are many objects we have seen in the real world that are circular in shape. Some of the examples are:

• Ring
• CD/Disc
• Bangles
• Coins
• Wheels
• Button
• Dartboard
• Hula hoop

We can observe many such examples in our day to day life.

There are many parts or components of a circle that we should know to understand its properties. A circle has mainly the following parts:

Circumference: It is also referred to as the perimeter of a circle and can be defined as the distance around the boundary of the circle.

Radius of Circle: Radius is the distance from the center of a circle to any point on its boundary. A circle has many radii as it is the distance from the center and touches the boundary of the circle at various points.

Diameter: A diameter is a straight line passing through the center that connects two points on the boundary of the circle. We should note that there can be multiple diameters in the circle, but they should:

• pass through the center.
• be straight lines.
• touch the boundary of the circle at two distinct points which lie opposite to each other.

Chord of a Circle: A chord is any line segment touching the circle at two different points on its boundary. The longest chord in a circle is its diameter which passes through the center and divides it into two equal parts.

Tangent: A tangent is a line that touches the circle at a unique point and lies outside the circle.

Secant: A line that intersects two points on an arc/circumference of a circle is called the secant.

Arc of a Circle: An arc of a circle is referred to as a curve, that is a part or portion of its circumference.

Segment in a Circle: The area enclosed by the chord and the corresponding arc in a circle is called a segment. There are two types of segments – minor segment, and major segment.

Sector of a Circle: The sector of a circle is defined as the area enclosed by two radii and the corresponding arc in a circle. There are two types of sectors – minor sector, and major sector.

For better understanding observe the given image depicting all parts of a circle.

Concentric circles are circles with the same or common center. In other words, if two or more circles have the same center point, they are termed as concentric circles. 

Let us move ahead and learn about some interesting properties of circles that make them different from other geometric shapes. Here is a list of properties of a circle:

• A circle is a closed 2D shape that is not a polygon. It has one curved face.
• The outer line of a circle is at equidistant from the centre.
• The diameter of the circle divides it into two equal parts.
• Circles which have equal radii are congruent to each other.
• Circles which are different in size or having different radii are similar.
• The diameter of the circle is the largest chord and is double the radius.
• Two circles can be called congruent if they have the same radius.
• Equal chords are always equidistant from the center of the circle.
• The perpendicular bisector of a chord passes through the center of the circle.
• When two circles intersect, the line connecting the intersecting points will be perpendicular to the line connecting their center points.
• Tangents drawn at the endpoints of the diameter are parallel to each other.

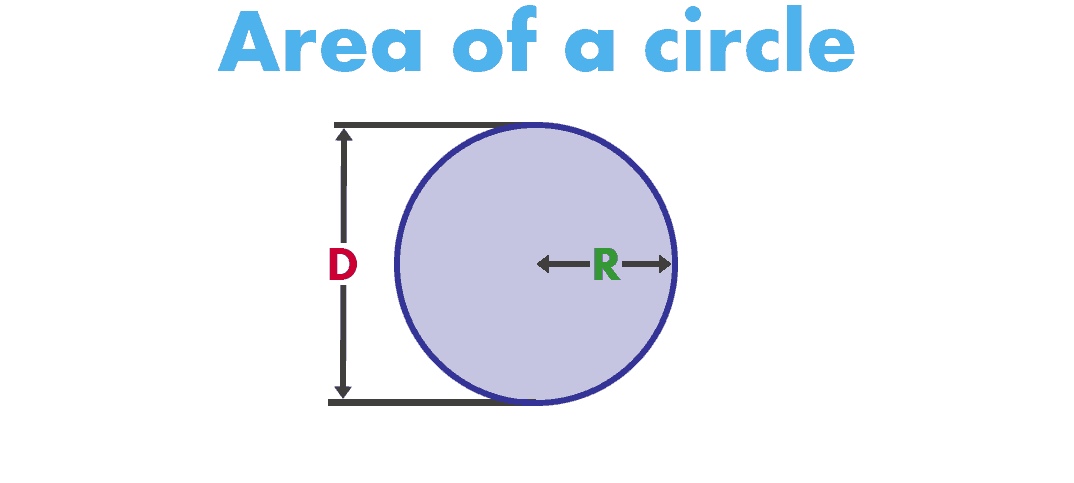
Area of a Circle Formula: 

The area of a circle refers to the amount of space covered by the circle. It totally depends on the length of its radius → Area = πr² square units.

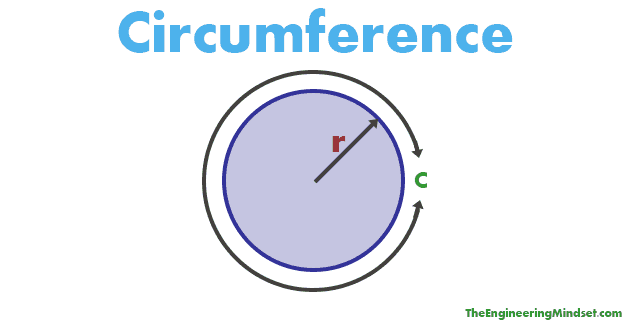
Circumference of a Circle Formula: 

The circumference is the total length of the boundary of a circle → Circumference = 2πr units.

Examples

Example 1:

Find the area and the circumference of a circle whose radius is 10 cm. (Take the value of π = 3.14)

Solution:

Given: Radius = 10 cm.

Area =π r² 

= 3.14  × 10²

A= 314 cm²

Circumference, C = 2πr

C= 2 ×3.14×  10 

Circumference= 62.8 cm

Example 2: 

Find the area of a circle whose circumference is 31.4 cm.

Solution:

Given:

Circumference = 31.4 cm

To find the area of a circle, we need to find the radius.

From the circumference, the radius can be calculated:

2 π r = 31.4

(2)(3.14)r = 31.4

r = 31.4 /(2)(3.14)

r=10/2 

r= 5

Therefore, the radius of the circle is 5 cm.

The area of a circle is πr² square units

Now, substitute the radius value in the area of a circle formula, we get

A = π(5)²

A = 3.14 x 25

A =  78.5 cm²

Therefore, the area of a circle is 78.5 cm².