Angles of Elevation and Depression
An angle of elevation is the “upward” angle from the horizontal to a line of sight from the object to a given point, whereas an angle of depression is where the angle goes “downward” from the horizontal to a given point, as shown below.
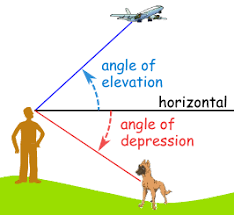
The term angle of elevation denotes the angle from the horizontal upward to an object. An observer’s line of sight would be above the horizontal.
The term angle of depression denotes the angle from the horizontal downward to an object. An observer’s line of sight would be below the horizontal.
Example:
Identifying the Angle of Elevation in a Diagram
In the given diagram of a ladder leaning against a wall, which of the following angles represents the ladder’s angle of elevation?
- ∠𝐵𝐴𝐶
- ∠𝐴𝐵𝐶
- ∠𝐴𝐶𝐵

Answer
The angle of elevation is the angle between the observer’s line of sight and the horizontal line (when the object is above the horizontal).
In this case, the angle of elevation is between the ladder and the horizontal (since there is no observer in this problem). This is highlighted in blue on the diagram below.

This angle is formed by the line segments 𝐴𝐵 and 𝐴𝐶 and is denoted as ∠𝐵𝐴𝐶 or ∠𝐶𝐴𝐵.
The answer is option A, ∠𝐵𝐴𝐶, since ∠𝐶𝐴𝐵 is not listed as an option.
Having learned how to identify the angle of elevation or depression within a diagram, we will next consider how to find unknown sides or angles in problems involving angles of elevation or depression.
We will focus on problems that involve right triangles, where the line of sight of the observer, the horizontal line, and the perpendicular distance of the object being observed from the horizontal line form a right triangle. This can be seen in the cases of elevation and depression below.
By using trigonometry and the Pythagorean theorem, we can determine the lengths and angles of these right triangles when given either two lengths or a length and the angle of depression or elevation. Let’s recall the trigonometric ratios.
Trigonometric Ratios
For a right triangle with a non-right angle 𝜃,a hypotenuse of length 𝐻,a side opposite to 𝜃 of length 𝑂,and a side adjacent to 𝜃 of length 𝐴,
sin𝜃 = 𝑂/𝐻, cos = 𝐴/𝐻, tan𝜃 = 𝑂/𝐴.
For the right triangles we create in angles of elevation or depression, we can label the sides by using the angle as follows: the hypotenuse is the line of sight of the observer, the adjacent side is the horizontal line, and the opposite side is the perpendicular distance of the object being observed from the horizontal. We can see this in the diagram below.
Since problems involving angles of elevation or depression usually involve the distance of the horizontal line from the observer to the point above or below the object being observed (the adjacent side), the perpendicular distance from the object to the horizontal line (the opposite side), and the angle of elevation or depression, we use the ratio for these lengths. This is the tangent ratio.



