Adding two or more binary numbers is one of the arithmetic operations on binary numbers or base-2 number systems. In decimal addition, when we add 3 + 2, we get 5. Similarly, when we add their binary equivalents, i.e (11)₂ and (10)₂, we get, (11)₂ + (10)₂ = (101)₂, which is 5 in base-10. The results of both binary and decimal addition give us the same answer, the only difference is in the place values of the digits. The process of binary addition will look very familiar to you, the only difference is that in the decimal number system we regroup the next place value whenever we get the sum of the digits greater than 9 because in the decimal system we use 10 digits from 0 to 9. But while adding binary numbers, we regroup the next place value when the sum of the digits becomes greater than 1 as, in the binary number system, only two digits can be used, and those are 0 and 1.

The four rules that apply when two binary digits are added are given below:

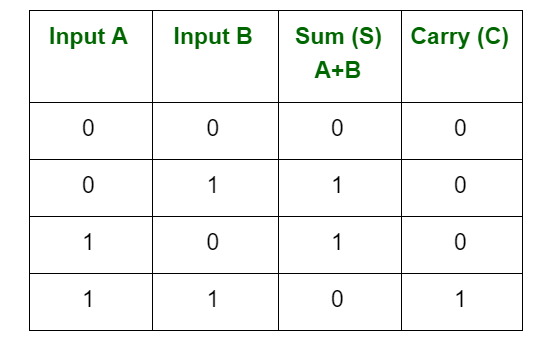
Now, let us use these binary addition rules to learn the process of adding binary numbers.

Example:

Binary numbers are used in computers to store and represent data using digits 0 and 1. There are two cases that come up while learning about binary addition, and those are given below:

• Binary addition without regrouping
• Adding binary numbers with regrouping

Binary Addition without Regrouping

When the addition of two digits results in 0 or 1, then we don’t need to regroup while adding two or more binary numbers. For example, let us add (101)₂ and (10)₂, which are the binary equivalents of 5 and 2 respectively.

Step 1: Write all the digits of both the numbers in separate columns as per their place values.

1 0 1
+ 1 0
———–
———–

Step 2: Start from the right-most column digits, 1 and 0. Apply one of the rules of binary addition which says 1 + 0 = 1.

1 0 1
+ 1 0
———–
1
————

Step 3: Move to the next column to the left. Here, we have two digits 0 and 1. Look at the rules given above and find out which rule will be applied here. Apply one of the binary addition rules which says 0 + 1 = 1.

1 0 1
+ 1 0
———–
1 1
————

Step 4: Now, in the last column, we have only 1 left, so we can apply the rule, 1 + 0 = 1. 

1 0 1
+ 1 0
———-
1 1 1
———-

Therefore, by adding (101)₂ with (10)₂, we get (111)₂ as the final answer.

Adding Binary Numbers with Regrouping

When the addition of two digits results in a number greater than 1, then we need to regroup while adding two or more binary numbers. For example, let us add (1001)₂ and (111)₂, which are the binary equivalents of 9 and 7 respectively.

• Step 1: Arrange the numbers as shown below.
• Step 2: Follow the binary addition rules to add the numbers. First let us add the digits in the one’s place, which are 1 + 1 = 0 (1 carryover). Here, 1 + 1 is 10, which is the binary equivalent of (2)₁₀, so we are regrouping the twos column by taking 1 as a carryover.
• Step 3: Now, we move to the next place value towards left, which is twos place. Here, we have 0 + 1 + 1 (carryover) = 10. So, again we will write 0 and take 1 as a carryover to the next place value. In the next column, we have 0 + 1 + 1 = 10. Similarly, we again take 1 as a carryover to the next column. In the last column to the left, we have 1 + 1 (carryover) = 10.

Therefore, (1001)₂ + (111)₂ = (10000)₂.