To visualize set operations, we will use Venn diagrams. In a Venn diagram, a rectangle shows the universal set, and all other sets are usually represented by circles within the rectangle.

The shaded region represents the result of the operation.

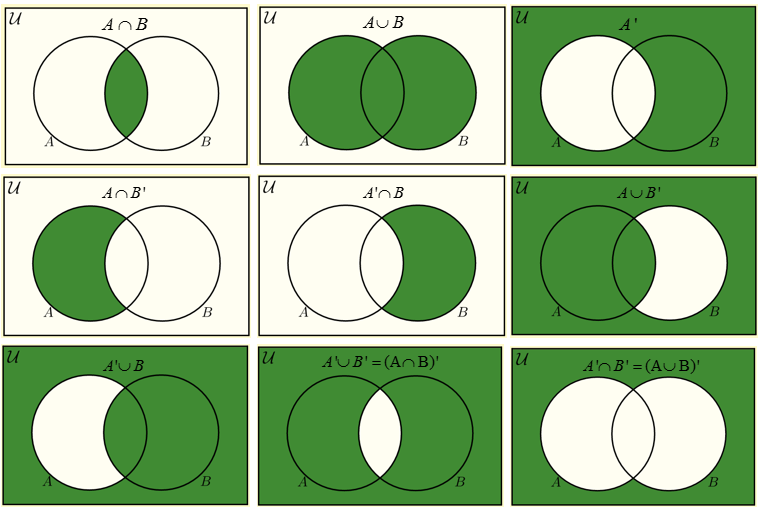
Examples

Union of sets using Venn diagram:

If A = {2, 5, 7} and B = {1, 2, 5, 8}. Find A U B using Venn diagram.

Solution:

According to the given question we know, A = {2, 5, 7} and B = {1, 2, 5, 8}

Now let’s draw the Venn diagram to find A union B.

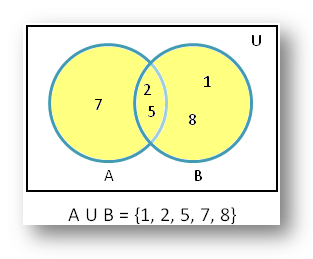
Therefore, from the Venn diagram we get A U B = {1, 2, 5, 7, 8}

From the adjoining figure find A union B.

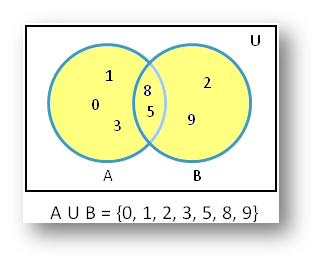
Solution:

According to the adjoining figure we get;

Set A = {0, 1, 3, 5, 8}

Set B = {2, 5, 8, 9}

Therefore, A union B is the set of elements which in set A or in set B or in both.

Thus, A U B = {0, 1, 2, 3, 5, 8, 9}

Intersection of sets using Venn diagram:

If A = {1, 2, 3, 4, 5} and B = {1, 3, 9, 12}. Find A ∩ B using Venn diagram.

Solution:

According to the given question we know, A = {1, 2, 3, 4, 5} and B = {1, 3, 9, 12}

Now let’s draw the Venn diagram to find A intersection B.

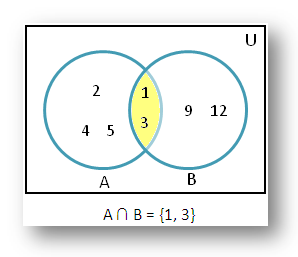
Therefore, from the Venn diagram we get A ∩ B = {1, 3}

From the adjoining figure find A intersection B.

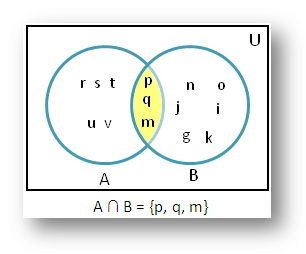
Solution:

According to the adjoining figure we get;

Set A = {m, p, q, r, s, t, u, v}

Set B = {m, n, o, p, q, i, j, k, g}

Therefore, A intersection B is the set of elements which belong to both set A and set B.

Thus, A ∩ B = {p, q, m}

Difference of sets using Venn diagram:

If A = {2, 3, 4, 5, 6, 7} and B = {3, 5, 7, 9, 11, 13}, then find (i) A – B and (ii) B – A.

Solution:

According to the given statement; A = {2, 3, 4, 5, 6, 7} and B = {3, 5, 7, 9, 11, 13}

(i) A – B

= {2, 4, 6}

(ii) B – A

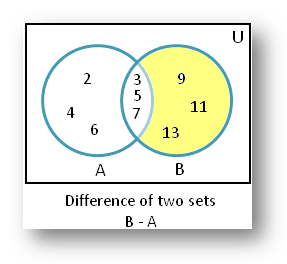
= {9, 11, 13}

Given three sets A, B and C such that: A = {x : x is a natural number between 10 and 16}, B = {set of even numbers between 8 and 20} and

C = {7, 9, 11, 14, 18, 20}. Find the difference of sets using Venn diagram:

(i) A – B

(ii) B – C

(iii) C – A

(iv) B – A

Solution:

According to the given statement

A = {11, 12, 13, 14, 15}

B = {10, 12, 14, 16, 18}

C = {7, 9, 11, 14, 18, 20}

(i) A – B

= {Those elements of set A which are not in set B}

= {11, 13, 15}

(ii) B – C

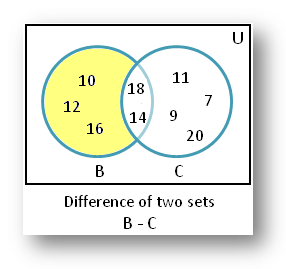
= {Those elements of set B which are not in set C}

= {10, 12, 16}

(iii) C – A

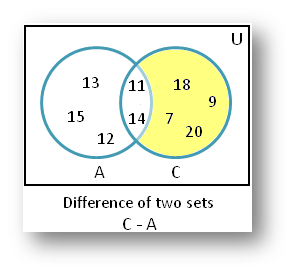
= {Those elements of set C which are not in set A}

= {7, 9, 18, 20}

(iv) B – A

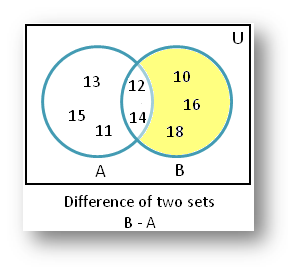
= {Those elements of set B which are not in set A}

= {10, 16, 18}