Ratio
A comparison of two numbers or quantities. They are measured in the same or similar units.
Example:
If the ratio of adults to children is 2 to 5, then there are two adults for every 5 children. So, if
there are 50 children in attendance, then there are 20 adults.
Ratios can be written in three ways: 2 to 5 2:5 2/5
The ratio is the comparison between two quantities in terms of their magnitudes. The ratio of two quantities a and b in some units is the fraction a/b and we write it as a: b. In the ratio a:b, we call ‘a’ the first term or antecedent and ‘b’, as the second term or consequent.
There are 3 blue squares to 1 yellow square
Ratios can be shown in different ways:
| Use the “:” to separate the values: | 3 : 1 | |
| Or we can use the word “to”: | 3 to 1 | |
| Or write it like a fraction: | 3/1 |
A ratio can be scaled up:
Here the ratio is also 3 blue squares to 1 yellow square, even though there are more squares.
Recipes
Example: A Recipe for pancakes uses 3 cups of flour and 2 cups of milk.
So the ratio of flour to milk is 3 : 2
To make pancakes for a LOT of people we might need 4 times the quantity, so we multiply the numbers by 4:
3×4 : 2×4 = 12 : 8
In other words, 12 cups of flour and 8 cups of milk.
The ratio is still the same, so the pancakes should be just as yummy.
“Part-to-Part” and “Part-to-Whole” Ratios
The examples so far have been “part-to-part” (comparing one part to another part).
But a ratio can also show a part compared to the whole lot.
Example: There are 5 pups, 2 are boys, and 3 are girls
Part-to-Part:
The ratio of boys to girls is 2:3 or 2/3
The ratio of girls to boys is 3:2 or 3/2
Part-to-Whole:
The ratio of boys to all pups is 2:5 or 2/5
The ratio of girls to all pups is 3:5 or 3/5
Scaling
We can use ratios to scale drawings up or down (by multiplying or dividing).
Example: To draw a horse at 1/10th normal size, multiply all sizes by 1/10th
This horse in real life is 1500 mm high and 2000 mm long, so the ratio of its height to length is
1500 : 2000
What is that ratio when we draw it at 1/10th normal size?
| 1500 : 2000 | = 1500×1/10 : 2000×1/10 | |
| = 150 : 200 |
We can make any reduction/enlargement we want that way.

Equivalent Ratios:
Two ratios are said to be equivalent if they represent the same value when reduced to the simplest form.
Examples of equivalent ratios:
- 1:2 , 2:4, 3:6
- 3:7, 6:14, 9:21
- 4:3, 8:6, 20:15
How to Identify Equivalent Ratios
Cross Multiplication Method
This method is convenient to use when the numbers involved are small.
Check whether 12:18 and 10:15 are equivalent ratios or not using the cross multiplication method.
Step 1: Write the given ratios in the fractional form that is numerator by denominator form.
![]()
Step 2: Cross multiply.
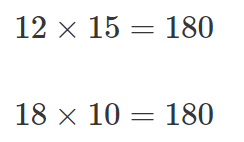
Step 3: If both products turn out to be equal, it would mean that the given ratios are equivalent ratios. Here,
![]()
Therefore, the given ratios (12:18 and 10:15) are equivalent ratios.
HCF Method
Let’s use the same example.
Step 1: We will find the HCF of the antecedent and consequent of both the given ratios.
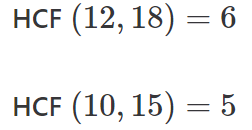
Step 2: Next, divide both the antecedent and consequent terms of both ratios by their respective HCF. So, we will get

Step 3: If the reduced forms of both the given ratios are equal, it means that the given ratios are equivalent. Here,
![]()
How to Find Equivalent Ratios?
If one of the ratios can be expressed as a multiple of the other given ratio, then they are said to be equivalent ratios. Thus, creating equivalent ratios is simple.
As is the case for equivalent fractions, we can easily find an equivalent ratio by multiplying the given ratio (both antecedent and consequent) with the same natural number.




