Addition and Subtraction
When we have two whole numbers:
– If both have the same sign, we add their absolute values and put the common sign:
3 + 4 = 7 – 3 – 4 = – 7
– If both have different signs, we subtract the bigger absolute value minus the lower absolute value and put the sign of the number which has bigger absolute value:
3 – 7 = – 4 11 – 7 = 4
When we have more whole numbers:
Just Add
Natural numbers ( etc.) are the numbers you see most often. They don’t have any fractions or decimals attached to them, and they exist above or to the right of on the number line.

Natural numbers are above zero on the number line.
When you add natural numbers, you just move up (or to the right) on the number line. For example, when you add you can start at :

Then, count up points. You can think of “” as sending a number to the right.

Adding means we stepped places up the number line, so .
Count Backwards
Subtracting a positive number from a positive number works the same way as adding a negative number to a positive number. It might help to conceptualize it a little differently, though. Let’s work with the expression .
First, let’s find all our numbers on the number line.

We’re working with 2 and 6
Since we’re subtracting from , we’re going want to use as our new anchor point and figure out ‘s position from it. So, let’s find ‘s position relative to .

Now, we’re subtracting . Subtracting a number is pretty much the same as adding the negative version of the same number, so we could rewrite our expression as . To find this, we can just flip ‘s position relative to :

Now, let’s just transpose to the same relative position to as it is to now.

As you can see from the image, you can also count backward on the number line to find the answer.
Now we can see that . When you subtract a number, you basically change its sign (so positive numbers become negative, and negative numbers become positive) and then add it as you would otherwise.
Examples
1. The girls had 3 weeks to sell tickets for their play. In the first week, they sold 75 tickets. In the second week they sold 108 tickets and in the third week they sold 210 tickets. How may tickets did they sell in all?
Solution:
Tickets sold in the first week = 75
Tickets sold in the second week = 108
Tickets sold in the third week = 210
Total number of tickets sold = 75 + 108 + 210 = 393
Answer: 393 tickets were sold in all.
2. Mr. Bose spent $450 for petrol on Wednesday. He spent $125 more than that on Thursday. How much did he spend on petrol on those two days.
Solution:
This problem has to be solved in two steps.
Step 1: Money spent for petrol on Thursday
450 + 125 = $575
Step 2: Money spent for petrol on both days
450 + 575 = $1025
3. Find the number, which is
(i) 1240 greater than 3267.
(ii) 1353 smaller than 5292.
Solution:
(i) The number is 1240 more than 3267
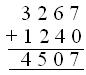
Therefore, the number = 3267 + 1240 or = 4507
(ii) The number is 1353 less than 5292
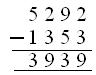
Therefore, the number
= 5292 – 1353 or
= 3939
6. The population of a town is 16732. If there are 9569 males then find the number of females in the town.
Solution:
|
Population of the town Number of males Therefore, number of females |
= 1 6 7 3 2 = – 9 5 6 9 = 7 1 6 3 |
7. In a factory there are 35,675 workers. 10,750 workers come in the first shift, 12,650 workers in the second shift and the rest come in the third shift. How many workers come in the third shift?
Solution: Number of workers coming in the first and second shift
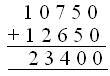
= 10750 + 12650 = 23400
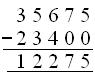
Multiplication
Multiplication is the repeated addition of a number. If we multiply m by n, that means m is repeatedly added to itself for n times. The symbol for multiplication is ‘×’.
For instance, 8 multiplied by 4 is equal to 32. How? Adding 8, 4 times to itself, we get;
8 + 8 + 8 + 8 = 32
Therefore, we can write,
8 x 4 = 32
Examples
Division
The division is a method of dividing or distributing a number into equal parts, For example, if 16 is divided by 4, then 16 is divided into 4 equal parts. Therefore, the resultant value is 4.
16 ÷ 4 = 4
Parts of division
Dividend ÷ Divisor = Quotient
15 ÷ 3 = 5
In the above example, there are three parts for division.
- 15 is dividend
- 3 is divisor
- 5 is quotient (R.H.S)
Examples
Multiplication and Division Relationship
Multiplication and division, are inverse operations of each other. If we say, a multiplied by b is equal to c, then c divided by b results in a. Mathematically, it can be represented as:
- a × b = c
- c ÷ b = a
For example,
- 4 x 5 = 20 [4 multiplied by 5 results in 20]
- 20 ÷ 5 = 4 [20 divided by 5 returns back 4]
Word Problems on Multiplication and Division
Q.1: There are 90 pencils in 1 box. How many pencils are there in 3 boxes?
Solution:
Given, 1 box has 90 pencils.
So, in 3 boxes, number of pencils = 3 x 90 = 270
Therefore, there are total of 270 pencils in 3 boxes.
Q.2: Rafay has 1615 candies stored in a box. If there are 85 such boxes, then how many candies are there in each box?
Solution:
Total number of candies = 1615
Number of boxes = 85
Therefore, each box contains = 1615 ÷ 85 candies
= 19 candies.


