A line is a fundamental concept in geometry. You could say it is the baby steps of a complex world, which is geometry.
A line segment is a portion of a straight line bounded by two points, called endpoints.
Consider the below diagram:

There are two points, they are denoted by A and B. In order to join both points, you need to draw a line, we call that type of line a line segment because it fulfils both conditions.
The first condition is the straight line, and the second condition is the two points. The line segment is denoted by the endpoints that limit it or a lowercase letter representing the line itself. There is not much rocket science in line segment that is why we called it baby steps because it is very simple and easy to understand.
Operations with Line Segments
You can apply mathematical operations within two or more line segments. Below are all the mathematical operations that you can apply on different line segments with their procedure.
Adding Line Segments

Subtracting Line Segments

Bisect a given Line Segment
Steps:
- Place the compass at one end of line segment.
- Adjust the compass to slightly longer than half the line segment length
- Draw arcs above and below the line.
- Keeping the same compass width, draw arcs from other end of line.
- Place ruler where the arcs cross, and draw the line segment.
Example:
Construct a perpendicular bisector of the given line segment AB.
Solution:
Step 1: Stretch your compasses until it is more then half the length of AB. Put the sharp end at A and mark an arc above and another arc below line segment AB.
Step 2: Without changing the width of the compasses, put the sharp end at B and mark arcs above and below the line segment AB that will intersect with the arcs drawn in step 1.

Step 3: Join the two points where the arcs intersect with a straight line. This line is the perpendicular bisector of AB. P is the midpoint of AB.
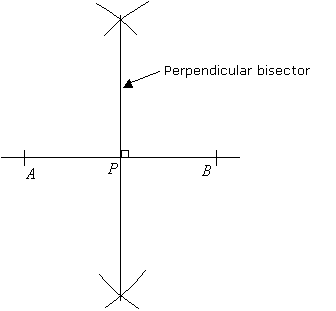
Draw a perpendicular to a line segment
The following diagrams show how to construct perpendicular lines through a point not on the line and through a point on the line.
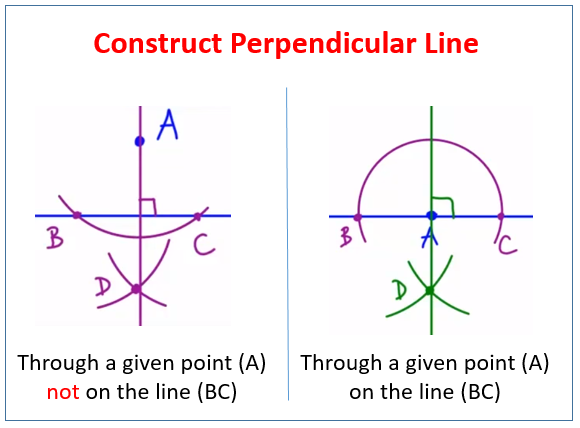
Using a Compass to construct perpendicular lines
Constructing perpendicular lines, looking at the two cases where the point is on the line, and the point is off the line.
How to Construct a Perpendicular Line through a Point on the Given Line?
- Open the compass to a radius less than half the segment.
- Draw two arcs intersecting the line on both sides of the point.
- Draw two arcs using the intersection points as the centers. Mark the point of intersection of the two arc.
- Construct a line between this point and the original point.