LCM by Listing Multiples 

Step 1: You need to list the multiples of each number until at least one of the multiples appears on all the lists.

Step 2: Now find the smallest number that is on all of the lists

Step 3: This number is the Least Common Multiple.

Example: Let’s find the LCM of (6,7,21)

Write down the multiples of 6:  6, 12, 18, 24, 30, 36, 42, 48, 54, 60

Write down the multiples of 7:  7, 14, 21, 28, 35, 42, 56, 63

Write down the multiples of 21: 21, 42, 63

Now you need to find the smallest number that is present on all of the lists. So the LCM(6, 7, 21) is 42.

LCM by Prime Factorization

Step 1: Firstly, find all the prime factors of each given number.

Step 2: Now, list down all the prime numbers found, as many times as these numbers occur most often for anyone given number.

Step 3: In step 3, you need to multiply the list of prime factors together to find the LCM.

Step 4: The LCM (a, b) can be calculated by finding the prime factorization of both the numbers a and b. We can do the same process for the LCM of more than 2 numbers.

For example, Let’s find the LCM (12,30) we find:

 12 = 2 × 2 × 3

 30 = 2 × 3 × 5

Therefore, the LCM (12,30) = 2 × 2 × 3 × 5 = 60.

How to calculate HCF?

There are three methods of how to find the highest common factor of any two or more given numbers:

1.  Factorization Method

2. Prime Factorization Method

3. Division Method

1. Factorization Method:

In the HCF  by factorization method, we find the greatest common factor by listing down the factors of the number.

Step 1: List down the factors of all the given numbers.

Step 2: Look for the highest factor among the listed factors which are common for both the given numbers. 

Let us take an example:

Example: Find the H.C.F, of 36 and 45.

Solution: 

36 = 1, 2, 3, 4, 6, 9, 12, 18, 36

45 = 1, 3, 5, 9, 45

Since the highest common factor of 36 and 45 is 9, therefore H.C.F of 36 and 45 is 9.

2. Prime Factorization Method (Tree Method):

Let us consider an example,

Step 1: In calculating the HCF by prime factorization, we factories the number into prime numbers, which are known as the prime factors.

Step 2: Start by dividing the given numbers by 2 (the first prime number), and go on dividing till you can’t divide the number any further.

Step 3: Finally, then write the numbers as a product of the prime numbers. The product of these common factors is the highest common factor of the given numbers.

Here’s an example for better understanding.

Find the HCF by prime factorization of the numbers 24 and 36.

Solution: 

To find the HCF by prime factorization,

24 = 2 x 2 x 2 x 3 x 1

36 = 2 x 2 x 3 x 3 x 1

Since the common factors of 24 and 36 are 2 x 3 x 2 x 1 = 12

Therefore, the HCF of the 24 and 36 is 12.

3. Division Method:

In the division method, we follow the following steps:

Step 1: Treat the smallest number as the divisor, and the bigger number as the dividend.

Step 2: Further divide the divisor by the remainder.

Step 3: Stop dividing when the remainder equals zero. 

Here’s an example,

Find the H.C.F of 12, 18.

Solution:

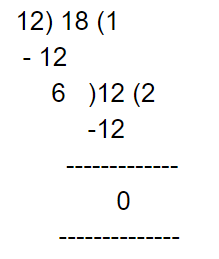
Here, 6 is the H.C.F.

How to find the HCF of 3 Numbers?

We can find the HCF of 3 numbers either by Prime Factorization Method or by Division Method. However, the steps for finding the highest common factor remain the same as above.

Here are a few highest common factor examples of how to find the highest common factor.

1. Find the HCF of 3 numbers 15, 30, and 90 using the Prime Factorization method.

The common factors here are 1,3,5.

Therefore, the highest common factor of the numbers,15,30, and 90 is 5×3×1=15.

Where are HCF and LCM used?