Binary Subtraction

Binary subtraction is the process of subtracting binary numbers. Binary numbers include only 0 and 1. The process of binary subtraction is the same as the arithmetic operation of subtraction that we do with numbers. Since only 0 and 1 are involved here, we may sometimes need to subtract 0 from 1. In such cases, we use the concept of borrowing as we do in an arithmetic subtraction. A binary number is expressed with a base-2. 

What is Binary Subtraction?

Can you subtract binary numbers? The answer is yes. Subtraction of binary numbers is an arithmetic operation similar to the subtraction of decimal numbers or base 10 numbers. For example, 1 + 1 + 1 = 3 in base 10 and 1 + 1 + 1 = 11 in binary number system. When you add and subtract binary numbers, you will need to be careful when borrowing as these will take place more often.

When you subtract several columns of binary digits, you must take into account the borrowing. When 1 is to be subtracted from 0, the result is 1 where 1 is borrowed from the next highest order bit or digit.

Binary Subtraction Rules

Rules and tricks: Binary subtraction is much easier than the decimal subtraction when you remember the following rules:

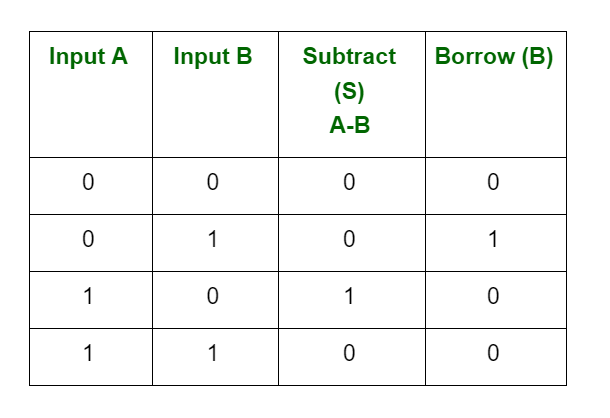
Now, look at the example of the binary subtraction: 101 from 1010

Decimal or base-10 numbers can be expressed as binary numbers. Binary numbers are used in computers to represent data since they understand only binary digits, 0 and 1. Let us understand how to subtract binary numbers with the example shown below.

Procedure to do Binary Subtraction:

1010

(-) 101

Step 1: First consider the 1’s column, and subtract the one’s column,( 0 – 1 ) and it gives the result 1 as per the condition of binary subtraction with a borrow of 1 from the 10’s place.

Step 2: After borrowing 1 from the 10’s column, the value 1 in the 10’s column is changed into the value 0

1 Borrow

1 0 1 0

(-) 1 0 1

——————

1

Step 3: So, subtract the value in the 10’s place, ( 0 – 0 ) = 0.

1 Borrow

1 0 1 0

(-) 1 0 1

——————

0 1

Step 4: Now subtract the values in 100’s place. Borrow 1 from the 1000’s place ( 0 – 1 ) = 1.

1 1 Borrow

1 0 1 0

(-) 1 0 1

——————

0 1 0 1

So, the resultant of the subtraction operation is 0101.

When you cross-check the binary subtraction resultant value with the decimal value, the resultant value should be the same.

The binary value 1010 is equal to the decimal value 10, and 101 is equivalent to 5

So, 10 – 5 = 5

Therefore, the decimal number 5 is equal to the binary number 0101.

Binary Subtraction Using 1’s Complement

• The number 0 represents the positive sign
• The number 1 represents the negative sign

Procedures for Binary Subtraction by 1’s Complement

• Write the 1’s complement of the subtrahend
• Then add the 1’s complement subtrahend with the minuend
• If the result has a carryover, then add that carry over in the least significant bit
• If there is no carryover, then take the 1’s complement of the resultant, and it is negative.

Example: Subtract ${\mathrm{100010_2\;}}_{}$from ${\mathrm{110101_2\;}}_{}$using 1’s complement method of binary subtraction.

Solution:

Step 1: Find the 1’s complement of the subtrahend, which is ${\mathrm{100010₂}}_{}$. The 1’s complement is ${\mathrm{011101₂}}_{}$.

Step 2: Add it with the minuend.

Step 3:

          0 1 1 1 0 1 
       + 1 1 0 1 0 1 
     ——————-
       1 0 1 0 0 1 0
    ——————–

Step 4: Here we get the last left-most digit 1 as a carryover. Now, we add it with the result obtained in step 3.

Step 5: Therefore, we get,

             0 1 0 0 1 0 
                         + 1
            —————-
             0 1 0 0 1 1
            —————-

The decimal equivalent of 100010₂ is 53 and the decimal equivalent of 110101₂ is 34. Therefore the result is 19. The binary equivalent of 19 is ${\mathrm{10011₂}}_{}$.

Example: (110101)₂ – (100101)₂

Solution:

(1 1 0 1 0 1)₂ = 53₁₀

(1 0 0 1 0 1)₂ = 37₁₀ – subtrahend

Now take the 1’s complement of the subtrahend and add with minuend.

1 carry

1 1 0 1 0 1

(+) 0 1 1 0 1 0

——————

0 0 1 1 1 1

1 carry

——————

0 1 0 0 0 0

Therefore, the solution is 010000.

Example: (101011)₂ – (111001)₂

Solution:

Take 1’s complement of the subtrahend

1 1 1

1 0 1 0 1 1

(+) 0 0 0 1 1 0 (1’s complement)

——————

1 1 0 0 0 1

Now take the 1’s complement of the resultant since it does not carry 1

The resultant becomes 0 0 1 1 1 0

Now, add the negative sign to the resultant value

Therefore the solution is – (001110)₂.