Course Content
Chapter 01 – Sets
A set is a list of objects in no particular order; they could be numbers, letters, or even words. A Venn diagram is a way of representing sets visually.
0/9
Set Notations
06:41
Game | Sets Match Up
05:00
Operations on Sets
09:44
Venn Diagrams
06:44
Game | Label the Venn Diagram
05:00
Operations on Sets through Venn Diagram
04:45
Game | Venn Diagram
05:00
Dare To Math
20:00
Math Lab
Chapter 02 – Rational Numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction p/q of two integers, a numerator p, and a non-zero denominator q. In this chapter, we will learn to represent rational numbers on a number line and perform arithmetic operations.
0/8
Rational Numbers
02:29
Game | Find the Match
05:00
Game | Rational vs. Irrational Numbers
05:00
Rational Number on Number Line
02:04
Game | Label Rational Number on Number Line
05:00
Operations on Rational Numbers
11:01
Dare To Math
20:00
Math Lab
Chapter 03 – Decimals
Decimals are a set of numbers lying between integers on a number line. They are just another way to represent fractions in mathematics. In this chapter, we will learn about the conversion of decimals to rational numbers, the kinds of decimals, and absolute values.
0/8
Conversion of Decimals to Rational Numbers
05:18
Game | Decimal Place Value
05:00
Game | Rational Number to Decimal
05:00
Terminating and Non-Terminating Decimals
05:40
Stimulation – Area Model Decimals
15:00
Approximate Value
02:28
Dare To Math
20:00
Math Lab
Chapter 04 – Exponents
The exponent of a number says how many times to use that number in a multiplication. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily. In this chapter, we are going to discuss the six important laws of exponents.
0/7
Base, Exponent and Value
02:07
Game | Exponent Group Sort
05:00
Game | Exponent Balloon Pop
05:00
Laws of Exponent
08:55
Game | Exponent Maze Chase
05:00
Dare To Math
20:00
Math Lab
Chapter 05 – Square Root of Positive Numbers
Square root, in mathematics, is a factor of a number that, when multiplied by itself, gives the original number. In this chapter, we will learn about what makes perfect squares and will find the roots of positive numbers by considering real-life scenarios.
0/5
Perfect Squares
03:04
Square Root
06:39
Game | Square and Roots Match Up
05:00
Dare To Math
20:00
Math Lab
Chapter 06 – Direct and Inverse Variation
Variation means change. With direct variation, numbers change proportionately in the same direction, while with inverse variation, they change in opposite directions. In this chapter, we will earn how to solve direct and inverse variation problems, explore their definitions, and work examples to understand the equations and techniques for solving them. Also, we learn to find the continued ratio for two or more ratios.
0/9
Continued Ratio
05:47
Direct Proportion
02:34
Stimulation – Proportion Playground
20:00
Inverse Proportion
05:54
Stimulation – Unit Rates
20:00
Game | Direct and Inverse Proportion
05:00
Time, Work, and Distance
08:42
Dare To Math
20:00
Math Lab
Chapter 07 – Financial Arithmetic
Financial mathematics describes the application of mathematics and mathematical modeling to solve financial problems. In this chapter, we will learn about the concept of taxation, profit/markups, zakat & ushr, and how they relate to our daily life.
0/7
Taxes
05:53
Profit and Markup
05:45
Game | Profit & Loss Wordsearch
05:00
Zakat
03:30
Ushr
05:50
Dare To Math
20:00
Math Lab
Chapter 08 – Algebraic Expressions
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The algebraic equations which are valid for all values of variables in them are called algebraic identities. In this chapter, we will learn to perform operations on polynomials and to factorize an algebraic equation by using identities.
0/13
Algebraic Expressions
09:55
Game | Expression Match Up
05:00
Stimulation – Expression Exchange
20:00
Polynomials
08:19
Game | Polynomial Group Sort
05:00
Addition and Subtraction of Polynomials
06:05
Multiplication and Division of Polynomials
05:59
Stimulation – Area Model Algebra
20:00
Algebraic Identities
06:35
Factorization of Algebraic Expressions
07:28
Game | Find the Factor Match
05:00
Dare To Math
20:00
Math Lab
Chapter 09 – Linear Equations
Linear equations are equations having variables with power 1. ax+b = 0 is an example with one variable where x is the variable, and a and b are real numbers. In this chapter, we will learn the definition, type of solutions, and how to solve these equations with one variable and two variables using different methods along with examples.
0/13
Game | Label the Equation
05:00
Linear Equations
02:15
Solution of Linear Equations
11:20
Game | Linear Magic Library
05:00
Stimulation – Equality Explorer
20:00
Game | Equation Match Up
05:00
Solving Equation with variables on both sides
07:36
Game | Detective X
05:00
Stimulation – Equality Explorer (Two Variables)
20:00
Solving Fractional Equations
02:23
Simulation – Balancing Equation
20:00
Dare To Math
20:00
Math Lab
00:00
Chapter 10 – Fundamentals of Geometry
Geometry is the study of different types of shapes, figures, and sizes in Maths or real life. In geometry, we learn about different angles, transformations, and similarities in the figures. It is important to know and understand some basic concepts. We will learn about working in different numbers of dimensions, and about some of the most fundamental concepts in geometry, including points, lines, and planes.
0/10
Properties of an Angle
02:53
Game | Angles
05:00
Congruent and Similar Figures
03:13
Game | Congruent VS Similar
05:00
Congruent Triangles
05:59
Game | Sort by Congruency
05:00
Circle
03:14
Game | Pin On the Circle
05:00
Dare To Math
20:00
Math Lab
Chapter 11 – Practical Geometry
The practical Geometry chapter will teach you about lines and to construct two-dimensional given different kinds of measurements. A quadrilateral is a closed two-dimensional shape that has four sides and four angles. Any four-sided closed shape such as square, rectangle, rhombus, parallelogram, trapezium, etc. And a closed two-dimensional shape that has 3 sides and 3 angles is known as a triangle.
0/17
Line Segments
02:56
Divide a Line Segment
09:31
Math Lab
Divide a Line Segment in a Given Ratio
09:55
Triangles
01:00
Game | Balloon Pop
05:00
Construction of a Triangle (Perimeters and Ratios Given)
07:52
Construction of an Equilateral Triangle
03:34
Construction of an Isosceles Triangle
10:21
Measures of a Triangle
07:14
Math Lab
Parallelogram
04:34
Game | Quadrilaterals Anagram
05:00
Construct a Parallelogram (Two Adjacent Sides Given)
06:42
Construction of a Parallelogram (Adjacent Side and Diagonal Given)
07:26
Measures of a Quadrilateral
02:30
Math Lab
Chapter 12 – Circumference, Area and Volume
This topic comes under analytical geometry and the formulas for the volume and the surface area of the sphere were first discovered by Archimedes. In this chapter, we will learn about the area and volume of two-dimensional and three-dimensional shapes.
0/8
Circumference and Area of a Circle
07:03
Game | Area of a Circle
05:00
Simulation – Surface Area
20:00
Surface Area of a Cylinder
03:08
Volume of a Cylinder
03:51
Game | Surface Area or Volume
05:00
Math Lab
Dare To Math
20:00
Chapter 13 – Information Handling
Frequency distribution, in statistics, is a graph or data set organized to show the frequency of occurrence of each possible outcome of a repeatable event observed many times. And, a pie chart is a way of representing data in a circular graph. Pie slices of the chart show the relative size of the data. In this chapter, we will learn to construct the frequency distribution table, some new pie chart vocabulary, and learn to construct the pie chart to represent the data.
0/8
Frequency Distribution
03:13
Bar Graphs
02:28
Game | Chart Labelling
05:00
Game | What Are Bars Telling?
05:00
Pie Chart
12:23
Game | Pin on the Pie
05:00
Dare To Math
20:00
Math Lab
Mathematics – VII
About Lesson

Parallelogram

A parallelogram is a two-dimensional geometrical shape, whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length. The Sum of adjacent angles of a parallelogram is equal to 180 degrees. In geometry, you must have learned about many 2D shapes and sizes such as circle, square, rectangle, rhombus, etc. All of these shapes have a different set of properties. Also, the area and perimeter formulas of these shapes vary from each other and are used to solve many problems. 

A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. Sum of all the interior angles equals 360 degrees.

Properties of Quadrilaterals - rectangle, square, parallelogram, rhombus, trapezium

A three-dimensional shape that has its faces in parallelogram shape, is called a parallelepiped. The area of parallelogram depends on the base (one of its parallel sides) and height (altitude drawn from top to bottom) of it. The perimeter of a parallelogram depends on the length of its four sides.

A square and a rectangle are two shapes which have similar properties of a parallelogram.

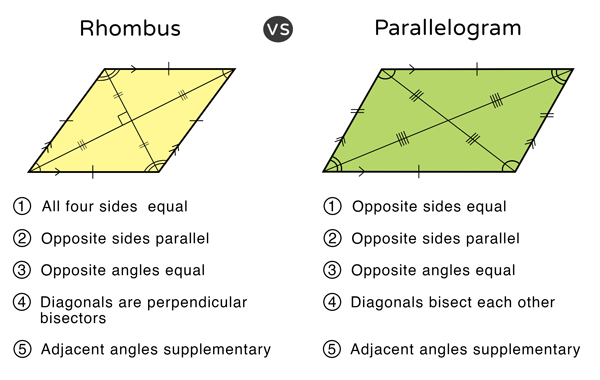
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.

Is a Rhombus a Parallelogram - Proof with Diagrams

Facts:

  • Number of sides = 4
  • Number of vertices = 4
  • Mutually Parallel sides = 2 (in pair)
  • Area = Base x Height
  • Perimeter = 2 (Sum of adjacent sides length)
  • Type of polygon = Quadrilateral

Special Parallelograms

Square and Rectangle: A square and a rectangle are two shapes which have similar properties of a parallelogram. Both have their opposite sides equal and parallel to each other. Diagonals of both shapes bisect each other. 

Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.

Rhomboid: A special case of a parallelogram that has its opposite sides parallel to each other but adjacent sides are of unequal lengths. Also, the angles are equal to 90 degrees.

Trapezium: If there is one parallel side and the other two sides are non-parallel, then it is a trapezium. 

Angles of Parallelogram

A parallelogram is a flat 2d shape which has four angles. The opposite interior angles are equal. The angles on the same side of the transversal are supplementary, that means they add up to 180 degrees. Hence, the sum of the interior angles of a parallelogram is 360 degrees.

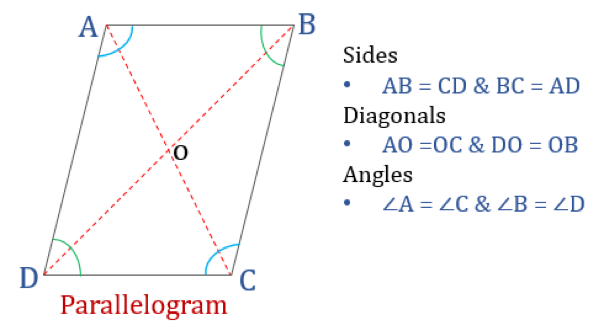
Properties of Parallelogram

If a quadrilateral has a pair of parallel opposite sides, then it’s a special polygon called Parallelogram. The properties of a parallelogram are as follows:

  • The opposite sides are parallel and congruent
  • The opposite angles are congruent
  • The consecutive angles are supplementary
  • If any one of the angles is a right angle, then all the other angles will be at right angle
  • The two diagonals bisect each other
  • Each diagonal bisects the parallelogram into two congruent triangles
  • The Sum of square of all the sides of parallelogram is equal to the sum of square of its diagonals. It is also called parallelogram law
Previous
Next
0% Complete